Trignometry Class 10 Maths

Trigonometry Ratios-Sine, Cosine, Tangent

The trigonometric ratios of a triangle are also called the trigonometric functions. Sine, cosine, and tangent are 3 important trigonometric functions and are abbreviated as sin, cos, and tan. Let us see how are these ratios or functions, evaluated in the case of a right-angled triangle.

Consider a right-angled triangle, where the longest side is called the hypotenuse, and the sides opposite to the hypotenuse is referred to as the adjacent and opposite.

The trigonometric ratios are calculated by the below formulas using above figure.

Functions	Abbreviation	Relationship to sides of a right triangle
Sine Function	sin	Opposite / Hypotenuse
Tangent Function	tan	Opposite / Adjacent
Cosine Function	cos	Adjacent / Hypotenuse
Cosecant Function	cosec	Hypotenuse / Opposite
Secant Function	sec	Hypotenuse / Adjacent
Cotangent Function	cot	Adjacent / Opposite

Trigonometry Angles

The trigonometry angles which are commonly used in trigonometry problems are  0°, 30°, 45°, 60° and 90°. The trigonometric ratios such as sine, cosine and tangent of these angles are easy to memorize. We will also show the table where all the ratios and their respective angle’s values are mentioned. To find these angles we have to draw a right-angled triangle, in which one of the acute angles will be the corresponding trigonometry angle. These angles will be defined with respect to the ratio associated with it.

For example, in a right-angled triangle,

Sin θ = Perpendicular/Hypotenuse

or θ = sin-1 (P/H)

Similarly,

θ = cos-1 (Base/Hypotenuse)

θ = tan-1 (Perpendicular/Base)

Trigonometry Table

Check the table for common angles which are used to solve many trigonometric problems based on trigonometric ratios.

Angles	0°	30°	45°	60°	90°
Sin θ	0	½	1/√2	√3/2	1
Cos θ	1	√3/2	1/√2	½	0
Tan θ	0	1/√3	1	√3	∞
Cosec θ	∞	2	√2	2/√3	1
Sec θ	1	2/√3	√2	2	∞
Cot θ	∞	√3	1	1/√3	0

Unit Circle

The concept of unit circle helps us to measure the angles of cos, sin and tan directly since the centre of the circle is located at the origin and radius is 1. Consider theta be an angle then,

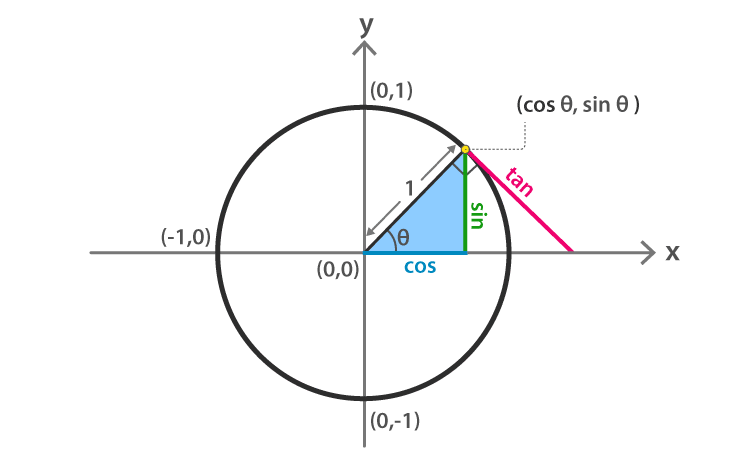
Suppose the length of the perpendicular is y and of base is x. The length of the hypotenuse is equal to the radius of the unit circle, which is 1. Therefore, we can write the trigonometry ratios as;

Sin θ	y/1 = y
Cos θ	x/1 = x
Tan θ	y/x

Trigonometry Formula

The Trigonometric formulas or Identities are the equations which are true in the case of Right-Angled Triangles. Some of the special trigonometric identities are as given below –

1. Pythagorean Identities

• sin ² θ + cos ² θ = 1
• tan 2 θ + 1 = sec2 θ
• cot2 θ + 1 = cosec2 θ
• sin 2θ = 2 sin θ cos θ
• cos 2θ = cos² θ – sin² θ
• tan 2θ = 2 tan θ / (1 – tan² θ)
• cot 2θ = (cot² θ – 1) / 2 cot θ

2. Sum and Difference identities-

For angles u and v, we have the following relationships:

• sin(u + v) = sin(u)cos(v) + cos(u)sin(v)
• cos(u + v) = cos(u)cos(v) – sin(u)sin(v)
• tan(u+v) = \(\frac{tan(u)\ +\ tan(v)}{1-tan(u)\ tan(v)}\)
• sin(u – v) = sin(u)cos(v) – cos(u)sin(v)
• cos(u – v) = cos(u)cos(v) + sin(u)sin(v)
• tan(u-v) = \(\frac{tan(u)\ -\ tan(v)}{1+tan(u)\ tan(v)}\)

3. If A, B and C are angles and a, b and c are the sides of a triangle, then,

Sine Laws

• a/sinA = b/sinB = c/sinC

Cosine Laws

• c2 = a2 + b2 – 2ab cos C
• a2 = b2 + c2 – 2bc cos A
• b2 = a2 + c2 – 2ac cos B

Applications of Trigonometry

• Its applications is in various fields like oceanography, seismology, meteorology, physical sciences, astronomy, acoustics, navigation, electronics, etc.
• It is also helpful to measure the height of the mountain, find the distance of long rivers, etc.

Trigonometry Problems and Solutions

Example 1: Two friends, Rakesh and Vishal started climbing a pyramid-shaped hill. Rakesh climbs 315 mtr and finds that the angle of depression is 72.3 degrees from his starting point. How high he is from the ground.

Solution: Let m is the height above the ground.

To find: Value of m

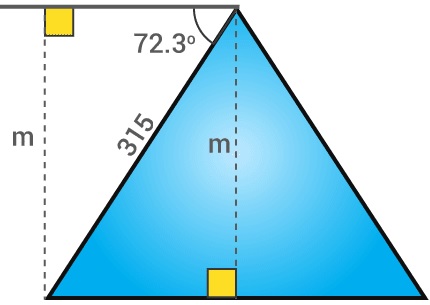
To solve m, use sine ratio.

Sin 72.30 = m/315

0.953 = m/315

m= 315 x 0.953

m=300.195 mtr

The man is 300.195 mtr above the ground.

Example 2: A man is observing a pole of height 55 foot. According to his measurement, pole cast a 23 feet long shadow. Can you help him to know the angle of elevation of the sun from the tip of shadow?

Solution:

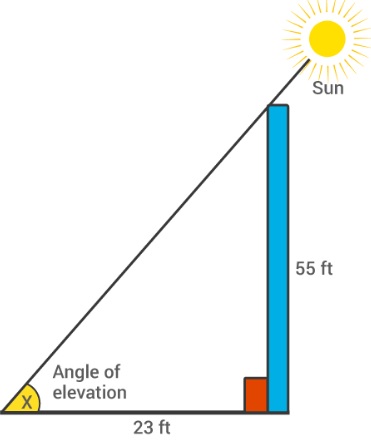
Let x be the angle of elevation of the sun, then

tan x = 55/23 = 2.391

x = tan-1(2.391)

or x = 67.30 degrees

Trigonometry Questions

Practice these questions given here to get a deep knowledge of Trigonometry. Use the formulas and table given in this article wherever necessary.

Q.1: In △ABC, right-angled at B, AB=22cm and BC=17cm. Find:

(a) sin A Cos B

(b) tan A tan B

Q.2: If 12cot θ= 15, then find sec θ?

Q.3: In Δ PQR, right-angled at Q, PR + QR = 30 cm and PQ = 10 cm. Determine the values of sin P, cos P and tan P.

Q.4: If sec 4θ = cosec (θ- 300), where 4θ is an acute angle, find the value of A.

Frequently Asked Questions

What do you Mean by Trigonometry?

Trigonometry is one of the branches of mathematics which deals with the relationship between the sides of a triangle (right triangle) with its angles. There are 6 trigonometric functions for which the relation between sides and angles are defined. Learn more all about trigonometry now by visiting BYJU’S.

What are the Different Trigonometric Functions?

There are 6 trigonometric functions which are:

• Sine function
• Cosine function
• Tan function
• Sec function
• Cot function
• Cosec function

......